The acoustic radiation field of organ pipes
C E Pykett
Posted:
13 October 2017
Revised:
25 October 2017
Copyright
© C E Pykett 2017
Abstract. This non-mathematical article shows that the surroundings of an organ pipe react so strongly on it that a flue pipe would not work at all if the adjacent atmosphere did not respond as it does, and reed pipes would sound completely different. Thus a pipe is not an isolated entity which operates independently of the environment it is in. The pipe-atmosphere interface is also responsible for its end corrections, and furthermore it influences radiating efficiency as a function of frequency. This affects the proportion of a pipe's sound energy contained in its early harmonics compared with the high ones, which strongly influences its subjective timbre or tone colour.
It is shown that all these effects follow from the fact that most of the pipe's energy does not propagate to long distances in the far field but instead it merely circulates closer to the pipe. In this near field region the energy is periodically stored in local air masses and then returned to the pipe during each oscillation cycle. The re-entry of energy causes the reflections which maintain the standing wave inside the pipe. The energy circulation process is also explained in terms of acoustic impedance, a term widely used but less well understood. An important aspect is that organ pipes must be poorly matched to their environment in terms of impedance if they are to function, thus they are inefficient generators of acoustic energy.
It is generally known that a flue pipe is a coupled system insofar as the intimate interaction between the air jet at its mouth and its resonant air column controls how it works. However it is less well appreciated that the interaction between the air column and the atmosphere is just as important. In other words an organ pipe is a triply-coupled system, the triplet being the air jet, the resonator and the atmosphere. It is therefore remarkable that one of the most ancient and apparently simple musical instruments is so complicated and whose secrets have yet to be fully revealed.
Contents
(click on the headings below to access the desired section)
Introduction
Sound radiation by the pipe - the piston analogy
Acoustic impedance
Near and far fields
Beam formation
End correction
Monopole and dipole radiation
Concluding remarks
Notes and References
Introduction
Several articles already on this site explain how organ pipes work (see references
[1] to [6]). However none cover what happens to the sound energy when it leaves the pipe but before it reaches our ears. This is just as important, because if the sound did not reach our ears we should have no musical instruments. The subject is also worth exploring for several other reasons, one of which is that a pipe's surroundings react so strongly on it that a flue pipe would not work at all if the surrounding atmosphere did not respond as it does. Another reason is that the topic is badly treated in the public domain literature. Much of what one finds on organ pipe acoustics and sound propagation is highly mathematical, and the usual level of treatment requires a physics degree if it is to be understood - this is literally true, not a joke. However things get worse, because the mathematical intractability of acoustics theory brings with it the need for simplifications if solutions to some equations are to be found, and these sometimes diverge wildly from experimental measurements. Yet, nothing daunted, theoreticians continue to build their edifices on such foundations as though the discrepancies did not exist. Putting it politely, the subject veers uncomfortably close to being scientifically disreputable at times. Therefore, not only is such material difficult to understand but it often describes reality rather badly once you have understood it, which makes the whole exercise somewhat pointless for practical purposes.
It was mentioned above that what goes on outside organ pipes influences strongly how they work inside and how they sound to a listener. A pipe is not an isolated entity which operates independently of the environment it is in. The pipe-atmosphere interface is responsible for its end corrections, and it also influences radiating efficiency as a function of frequency. This affects the proportion of a pipe's sound energy contained in its early harmonics compared with the high ones, which in turn strongly influences its subjective timbre or tone
colour. It is generally recognised that a flue pipe is a coupled system insofar as the intimate interaction between the air jet at its mouth and its resonant air column controls how it works
[1]. However it seems to be less well appreciated that the interaction between the air column and the atmosphere is just as important. In other words, an organ pipe is a triply-coupled system, the triplet being the air jet, the resonator and the atmosphere. It is therefore remarkable that one of the most ancient and apparently simple musical instruments is so complicated and whose secrets have yet to be fully revealed. Consequently this article attempts to throw more light on the resonator-environment interaction.
The article offers a different take on the matter to benefit those who are not physicists. It is not mathematical except for the odd simple formula here and there, and these can be ignored anyway without much loss of comprehension. Instead, it describes in terms of pictures what happens to sound when it emerges from both flue and reed organ pipes before we hear it. The approach is not unique because one can find similar information scattered elsewhere in the literature. However, as far as I am aware none of it discusses the acoustic radiation field set up by a pipe with the completeness to be found here. Here you have it all in one place.
Sound radiation by the pipe - the piston analogy
Organ pipes emit sound from either one or two apertures. Flue pipes always have a mouth, and if they are open at the top sound emerges from there as well. This also happens with reed pipes though these have no mouth, only an open top. As described in some of the previous articles mentioned already, an acoustic standing wave is set up in flue pipes which is either half a wavelength long for an open pipe, or a quarter of a wavelength for a stopped pipe (including the end corrections at the mouth and open end)
[1]. The resonators of reed pipes also support standing waves, but two other functions of the pipe body are to act both as an acoustic transformer and as a filter between the reed assembly and the atmosphere. The transformer action enhances the loudness of the naked reed itself, and the filter modifies its frequency spectrum
[2].
But in all cases, wherever there is an aperture which emits sound, one can assume that energy is drawn from the internal standing wave and emitted in phase at all points across the cross-section of the aperture. Thus the air in the aperture acts like a piston of the same size, vibrating slightly to and fro as a single entity with a fundamental frequency (pitch) equal to that of the sound produced by the pipe. The piston also vibrates at all the harmonics which largely determine the timbre or tone colour of the pipe. The same piston analogy is used when considering a loudspeaker cone, at least at medium and low frequencies. However unlike a loudspeaker, the piston here is not made of relatively rigid material of course. Although moving as one entity across the aperture of a pipe, the motion is still one which comprises nothing but air having the elasticity and density of the atmosphere, and the use of the word 'piston' does not imply any other substance.
Acoustic impedance
Acoustic impedance is a term you need to be aware of because it crops up repeatedly, both in this article and in the literature. But basically it's nothing but Ohm's Law applied to sound rather than to electrical circuits.
The standing wave inside the pipe is created from two wave motions travelling in opposite directions, which in turn are maintained through reflections occurring at both ends regardless of whether they are open or closed. This was explained in more detail in reference
[1]. At an aperture such as an open end the air pressure in the wave falls to a low, though not zero, value because a high pressure could not continue to exist in the atmosphere at large. This means there is a sudden reduction in acoustic impedance at an open end, because impedance equals pressure divided by volume flow rate (essentially the number of air molecules vibrating across the open end). This is analogous to electrical impedance which equals voltage (the electromotive force) divided by current (the rate of electron flow).
Impedance in both acoustic and electrical systems consists of two parts. One is purely 'resistive', analogous to an electrical resistor having a resistance of so many ohms. The other part is purely 'reactive' and it represents the opposition to air flow caused by having to move air masses around or by compressing the air itself. These matters become more complicated the further you delve into them, but for now it is sufficient to know that energy is dissipated or lost in a resistance whereas it is not lost in a reactance. For organ pipes, the resistive element of impedance determines the amount of sound energy which propagates into the atmosphere beyond the pipe and which we hear as its sound. This variety of resistance is called the 'radiation resistance' against which the pipe has to work. The reactive element represents air movement close to the pipe. This motion does not propagate or dissipate any energy from the pipe; rather the 'reactive' air just moves around locally as described in the next section. During each cycle of oscillation it temporarily stores energy from the pipe and then gives it back again.
Because of the impedance change, and hence the sudden changes in pressure and flow rate, one cannot assume that the sound wave emerging from the end or mouth of the pipe simply continues to propagate indefinitely into the atmosphere as though nothing had happened. Although some of the wave's energy does continue to propagate, one can imagine the emerging wavefront from the air piston to be subjected to a kind of shock which causes it to change its character. The changes are sudden and dramatic and they lead to the formation of what is called a near field wave in the atmosphere. This begins at the pipe aperture and it eventually morphs into a far field wave which propagates into the surroundings. It is the far field wave which we hear at some distance from the pipe. These fields will now be discussed further.
Near and far fields
We saw above that an air piston at the pipe aperture pushes and pulls on the air molecules in the atmosphere just outside the pipe which are closest to it. What happens now is dominated by one factor, which is energy storage and release in air.
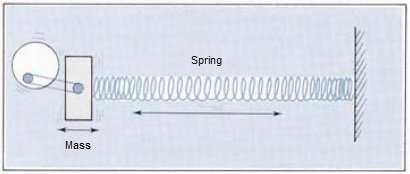
Figure 1. Energy storage in a mass-spring system
Air is perhaps surprisingly massive, having a density equivalent to three cans of baked beans sitting inside a
metre-cubed cupboard. Less surprising, because it is better-known, is that air is also elastic in that it can be compressed and rarefied. Both these properties enable it to store and then release energy. Referring to Figure 1, the rotating crank at the left hand side corresponds to the oscillating air piston at an aperture of an organ pipe. It is depicted transferring its motion to a mass which in turn compresses and extends a spring. The mass and springiness are those of the air in the atmosphere in contact with the air piston at the pipe aperture. As the air mass is moved back and forth by the piston, it periodically stores and releases kinetic energy over each oscillation cycle. Similarly, as the air spring moves it periodically stores and releases potential energy. The system is analogous to an electrical circuit in which mass corresponds to inductance and springiness to capacitance - both of these electrical components store and release energy in a similar way. Do not worry if you are unfamiliar with the difference between kinetic and potential energy. It is sufficient to know that a volume of air can store and release energy when it is repetitively pushed and pulled.
So what, you might ask. It's a good question because in fact nothing much happens other than the air just outside the pipe aperture gets pushed and pulled as the piston oscillates. But the point is that relatively little of the piston's energy propagates away from the pipe into the far distance, though the fact that a minority does is important otherwise nothing would be heard at all. Nevertheless, at any instant in an oscillation cycle the majority of the energy imparted by the piston to the surrounding air may be travelling away from the pipe, but at a later instant it will reverse direction and return. Most of the piston's energy is stored, released and it moves around but little of it propagates, thus only a small proportion of the energy from the air piston propagates away. When the energy is released from storage it goes back into the pipe. The flue pipe is a classic example of an impedance mismatch between a generator (the pipe itself) feeding an antenna (the pipe aperture) feeding the environment (the room). The mismatch arises because no attempt is made to match the pipe to its surroundings, unlike a radio transmitter where it is vital to match the transmitter to the antenna to maximise the signal strength at a distant receiver. The pipe could be matched using a horn, but then it would cease to work because its action depends on reflections occurring at both ends. These reflections arise from the energy stored externally which is periodically fed back into the pipe during each oscillation cycle. If the pipe were to be matched to the atmosphere there would be no external energy storage. All its internal energy would then propagate away rapidly and it would not speak.
Reed pipes are different because the reed and shallot assembly can emit sound independently of the resonator tube and of the atmosphere beyond it. So one function of the resonator is to match the high output impedance of the reed to the lower input impedance of the atmosphere - it acts as an acoustic transformer, not unlike a horn, as mentioned already. This is why the resonating tubes of many reed pipes are conical, flaring outwards to approximate to a horn. But even here the match must not be too good because the resonator would not resonate otherwise. It still needs to retain a retinue of natural resonant frequencies in the same way that a flue pipe does. In both cases the resonances of the air column filter and shape the harmonic spectrum generated at the mouth of a flue pipe, or at the reed of a reed pipe, to endow the sounds with much of the beauty we expect from organ pipes.
So both types of pipe must have an impedance mismatch between their radiating apertures and the atmosphere, and this results in the behaviour described above where most of the pipe's energy circulates locally rather than propagating away. The part of the acoustic field where all this occurs, close to the pipe, is called the near field. If you stuck your head into the near field you would hear sound, just as you would if you stuck it close to a loudspeaker where much the same effects arise. But most of what you would hear does not propagate very far. The situation is sketched in Figure 2.
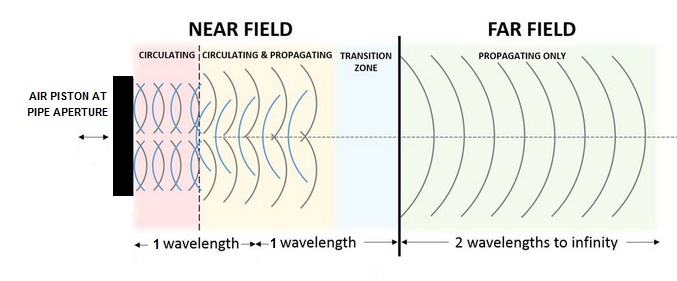
Figure 2. Near and far acoustic fields
The diagram illustrates the circulating energy region in the near field described above, which progressively gives way to the far field where all the energy is propagating. This evolution happens for two reasons. The first reason relates to a clue given above - although the majority of the energy close to the air piston does indeed merely circulate in and out of the pipe, there is nevertheless a minority which propagates away into the distance. The second reason is that eventually the more distant circulating air molecules start to escape the push-pull influence of the piston - the periodic compression and suction exerted by the piston begins to dissipate as the distance from it increases. This effect takes place in what is called the 'transition zone' between the near and far fields. Thus the circulating field eventually dies away to leave only the propagating energy, all of which flows into the distance and it allows us to hear the organ pipe speaking. Referring back to the previous section dealing with impedance, the energy in the far field is that dissipated in the resistive component of the impedance 'seen' by the air piston at the pipe aperture. Most of that in the near field is represented by the reactive component of impedance. This reactive energy is not dissipated or lost, it merely circulates locally in and out of the pipe as described above while the pipe is speaking, but eventually the circulation disappears with increasing range from the pipe
[9].
The near and far fields are vaguely defined in spatial extent. There is no specific point at which one can say the near field ends and the far field begins as one moves away from the pipe. However it does depend partly on the size of the source relative to the wavelength of the sound being radiated. All organ pipes are 'acoustically small', which means that the dimensions of the radiating apertures (the mouth and top of the pipe) are much smaller than the wavelength. This can be appreciated by remembering that the speaking length of an open pipe is nearly half a wavelength, thus the wavelength of the sound emitted by such a pipe is about twice its height (ignoring the pipe foot). This is always very much larger than both its mouth dimensions and the diameter at the top, the two apertures where its sound emission occurs. For acoustically small sound sources the near field is generally assumed to extend about one wavelength from the source, and the far field is reckoned to start at about two wavelengths. The region in between, extending from one wavelength to two, is conventionally said to be the transition region between the two fields. These distances obviously become very large for the lowest-pitched pipes in an organ. For instance, the wavelength of an open 32 foot pipe is 64 feet. Therefore the far field of this pipe does not nominally begin until you get 128 feet away from it, about 43 yards or 40
metres. This exceeds the width of the nave of St Paul's cathedral in London! Consequently you will frequently be within the near field of the lowest notes of an organ even in the largest buildings, and this partly explains the well-known quirkiness associated with deep bass pipes. At one point you often find that they might produce that intense visceral flutter which some enjoy, yet at another they can be virtually inaudible. This is partly a result of the dramatic changes in amplitude and phase which occur throughout the near field of any acoustic source. (These effects are in addition to those due to room resonances and multipath propagation caused by reflections). The phenomenon was in evidence when I played at Exeter cathedral, where bottom C on the 32 foot Contra Violone stop was distinctly muted at the console yet it produced much rattling of windows and furniture elsewhere in the building!
A necessary remark at this point is to repeat that the foregoing refers to acoustically small sound sources, which applies to the fundamental frequency of all organ pipes and their early harmonics where the wavelengths are large compared with the sizes of mouth and top. However some string toned flue pipes and some reed pipes have a harmonic retinue extending to the fiftieth or beyond, and in these cases the higher harmonics have very much smaller wavelengths. Wavelengths at these high frequencies can be comparable with the dimensions of the radiating apertures, and this means the system is no longer acoustically small. Two points follow from this. The first is that the near and far field distance milestones in terms of wavelength differ from those just described. The second is more important for present purposes, because the proportion of energy which propagates directly away from the air piston is much greater than at the lower frequencies. Instead of being far less than the circulating energy it is now typically comparable with it. The practical result is that the highest harmonics of some organ pipes are radiated with much greater efficiencies than the fundamental and lower ones. This contributes to the strong high harmonics heard in the sounds of string and reed pipes, which significantly influence their characteristic tone colours or timbres. In terms of impedance, the impedance match between the pipe and its speaking environment at high frequencies gets much better than at low ones.
Beam formation
Owing to the phenomenon of diffraction, sound emerging from apertures can sometimes form narrow beams in space rather than it being isotropic or
omnidirectional, and it is often said that this also occurs for organ pipes. For interest's sake a nice example of an acoustic beam is shown below in Figure 3, though nothing like this occurs with organ pipes for reasons to be described (the example relates to a sonar transducer used in underwater acoustic surveys).
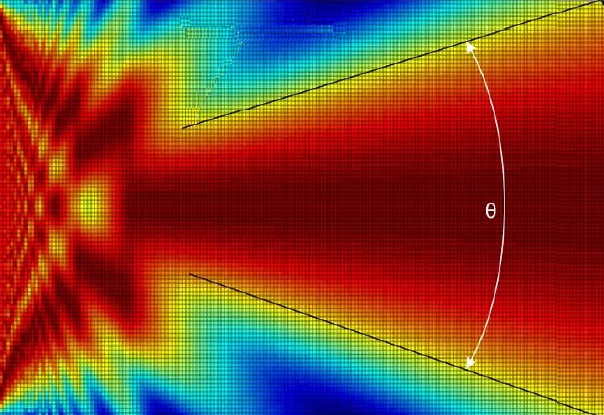
Figure 3. Computer simulation of an acoustic beam of angular width
θ emerging from an acoustically large source on the left
(© Kongsberg Mesotech Ltd)
The angular width of the beam is
θ (theta), and this depends on the ratio
λ/D where λ (lambda) is the wavelength of the sound and D is the linear size (e.g. the diameter) of the aperture. When this value is large, which means
λ is much greater than D, there is no tendency for beams to form. Beam formation only occurs when
λ is considerably less than D, and for the example pictured above
λ/D = 0.023. The reciprocal of this figure, which means calculating
D/λ instead of
λ/D, shows that there are about 43 wavelengths across the radiating aperture to the left of the picture. This means the source was acoustically large relative to the wavelength. Therefore this is a very different situation to that for organ pipes. In these cases, wavelengths at the fundamental frequency and the early harmonics are always much larger than the dimensions of the radiating apertures of a pipe, because pipes are acoustically small at these frequencies as we saw in the previous section. Therefore the quantity
λ/D is always much greater than one at these relatively low frequencies, not less than one. Typically its value at the top of an open pipe, where D equals the pipe diameter, varies from around 15 for flute pipes to 50 or so for strings. Consequently there is no tendency for pipes to form beams and we can therefore assume they radiate
omnidirectionally. Only the highest few harmonics in the narrowest string and possibly some reed pipes are likely to form beams, and even then the beams will still be relatively wide, far wider than that shown in Figure 3.
Incidentally, the left hand side of the picture also eloquently illustrates the messiness of the near field and the way it dies away to leave only the far field.
End correction
It is well known that organ flue pipes seem to be longer than they are in that they emit sound with a frequency somewhat lower than their lengths would suggest. The difference is conventionally attributed to an end correction, and I have treated the subject in detail in an article at reference
[7]. The point was made there that the term is unfortunate because it obscures the true explanation of the effect. What actually causes the frequency reduction is the mass of a lump of air in the atmosphere just outside the radiating apertures of the pipe at its mouth and top (if open), and we are now in a position to better appreciate the situation.
In the earlier section dealing with the near field close to the pipe, the 'reactive' transfer of energy in and out of the pipe was described. It was explained how some of the energy emerging from the pipe (in fact the majority of it) does not propagate into the far distance. Instead the energy gets temporarily stored, partly through moving some of the air around and partly through compressing and expanding it. The stored energy is released during a subsequent part of each oscillation cycle and given back to the pipe - it is not lost and it does not propagate away. The first effect, moving the air around, stores energy in its mass and the second effect stores energy in its springiness. Any moving mass has stored energy, as you discover when you walk into a door which is closing against you, and as far as end corrections are concerned it is mass we are interested in here. This is because the longitudinal waves in an organ pipe can be represented as a series of many small masses joined by springs, which represent the density and springiness of air respectively. The arrangement is sketched in Figure
4 [10].
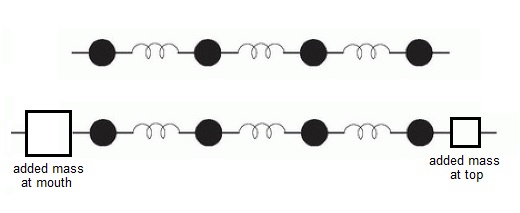
Figure 4. Illustrating the added masses at the speaking orifices of an organ pipe
The upper part of the diagram just shows the masses which oscillate horizontally when the pipe is speaking. Below are shown the added masses in the atmosphere outside each speaking orifice, and they are deliberately of different sizes because the effective mass at the mouth is greater than at the top for reasons we shall not go into here (it is discussed in reference
[7]). Therefore it should come as no surprise that an extra lump of air at the pipe mouth and at its open end will lower the frequency at which the whole system oscillates. The lumps of air are those involved in the circulating energy storage taking place in the near field regions in proximity to the pipe apertures. They are in intimate communication with the mass of air inside the pipe body because they periodically give back their energy to the pipe after they have just temporarily absorbed it from the oscillating air piston.
It is possible to calculate the masses of these lumps, and once this has been done it is then possible to calculate by how much the pipe's frequency will be lowered. The first part of this calculation is difficult whereas the second part is easy, but fear not - we shall not attempt either step here. But if you persevere with the calculation you come up with an equation which predicts the end correction for any pipe of given dimensions. Unfortunately, most of those who have done it have got it spectacularly wrong. I applied one well known equation found in the literature
[8], apparently much loved of theoreticians, to predict the end correction at the mouth of the pipe described in the article mentioned previously
[7]. My measurements showed it to be 143 mm versus a predicted value of 80 mm. Not very impressive, you might rightly conclude!
Monopole and dipole radiation
Stopped flue pipes and reed pipes have only one radiating aperture and they radiate omnidirectionally as so-called acoustic monopoles. Nothing more needs to be said about these as their pertinent characteristics have been covered already. But open flue pipes are acoustic dipoles, meaning that they radiate from two apertures. Moreover, the radiated waves are in phase with each other at the fundamental frequency and the odd-numbered harmonics, but out of phase at the even harmonics. The effect gives rise to a theoretical cancellation effect at certain angles, especially for a few of the early (even) harmonics. However, in practice this is only noticeable in an anechoic environment and at short distances from the pipe. In real rooms and at realistic listening distances there is so much environmental mixing of the energy from the two apertures that the acoustic power as a function of direction becomes unimportant. Room acoustics such as resonant modes (standing waves) and multipath propagation due to reflections from surfaces are the dominant factors in practice.
Concluding remarks
This article has shown that the surroundings of an organ pipe react so strongly on it that a flue pipe would not work at all if the adjacent atmosphere did not respond as it does, and reed pipes would sound completely different. Thus a pipe is not an isolated entity operating independently of the environment it is in. The pipe-atmosphere interface is also responsible for its end corrections, and furthermore it influences radiating efficiency as a function of frequency. This affects the proportion of a pipe's sound energy contained in its early harmonics compared with the high ones, which strongly influences its subjective timbre or tone
colour.
It was shown that all these effects follow from the fact that most of the pipe's energy does not propagate away to long distances in the far field but instead it merely circulates closer to the pipe. In this near field region the energy is periodically stored in local air masses and then returned to the pipe during each oscillation cycle. The re-entry of energy causes the reflections which are conventionally interpreted as maintaining the standing waves inside the pipe. The process was also explained in terms of acoustic impedance, a term widely used but less well understood. An important aspect is that organ pipes must be poorly matched to their environment in terms of impedance so they will work as expected, thus they are inefficient generators of acoustic energy.
It is generally known that a flue pipe is a coupled system insofar as the intimate interaction between the air jet at its mouth and its resonant air column controls how it works. However it is less well appreciated that the interaction between the air column and the atmosphere is just as important. In other words an organ pipe is a triply-coupled system, the triplet being the air jet, the resonator and the atmosphere. It is therefore remarkable that one of the most ancient and apparently simple musical instruments is so complicated and whose secrets have yet to be fully revealed.
Notes and references
1.
"How the flue pipe speaks",
an article on this website, C E Pykett, 2001.
2. "How the reed pipe speaks", an article on this website, C E
Pykett, 2009.
3. "The Tonal Structure of Organ
Flute Stops", an article on this website, C E Pykett, 2003.
4. "The Tonal Structure of Organ Principal
Stops", an article on this website, C E Pykett, 2006.
5. "The Tonal Structure of Organ
String Stops", an article on this website, C E Pykett, 2012.
6. "The Tonal Structure of Organ Reed Stops",
an article on this website, C E Pykett, 2011.
7. "The End Corrections, Natural Frequencies, Tone Colour and Physical Modelling of Organ Flue
Pipes", an article on this website, C E Pykett, 2013.
8. "Some measurements of the end-corrections and acoustic spectra of cylindrical open flue organ pipes", F Ingerslev and W
Frobenius, Trans. Danish Academy of Technical Sciences, vol 1, 1947.
9. The circulation of the reactive energy in the near field discussed in the article assumes that none of it is lost. It is true that none of it propagates into the far field because it would then form part of the resistive energy which radiates away into the distance. However in reality there will be some loss of circulated energy owing to friction between the air molecules and other factors arising in practice. This loss is converted into heat, but it represents only a small fraction of the total and it is therefore ignored here.
10.
In terms of energy storage in air, mass is more important than springiness as
far as organ pipes are concerned. For the pressures and flow rates
involved here, air can be taken as virtually incompressible. Relatively
little energy can be stored in the springiness of an incompressible fluid
compared with the kinetic energy stored in its mass.